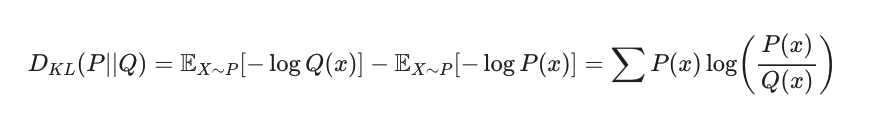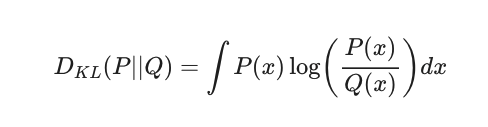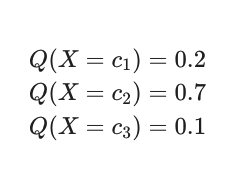ML/ML
정보이론 톺아보기
inistory
2021. 11. 8.
1. 정보이론이란?
- 추상적인 '정보'라는 개념을 정량화하고 정보의 저장과 통신을 연구하는 분야
2. 사건 x 의 정보량

3. Entropy
- 엔트로피는 특정 확률 분포를 따르는 사건들의 정보량의 기댓값이다.
- 이산확률변수 X가 x1,x2,…,xn 중 하나의 값을 가진다고 가정
- 기대값수식 부분에 확률 대신 정보량을 넣음

예제 1 : 공을 꺼낼 때 엔트로피를 계산해보자

- 엔트로피 = 무질서 = 불확실성
- 공의 종류가 다양할 때 엔트로피가 더 높다
예제 2: 공 색깔을 두 가지로 고정, 색 비율을 다르게 했을 때 엔트로피는?

- 확률변수가 가질 수 있는 가짓수가 같을 떄, 사건의 확률이 균등할수록 엔트로피 값은 증가한다.

- 동전이 앞면 나올 확률 50%, 뒷면 나올 확률 50% 일 때가 앞면이 나올 확률이 90%인 동전을 던질 때보다 결과를 예측하기 어렵기 때문에 엔트로피(불확실성)가 크다.
- 따라서 균등분포일 때 엔트로피가 최대이다.
3.2 연속 확률 변수(Continuous Random Variables) 인 경우

- 확률 변수 X의 확률 밀도 함수가 p(x)일 때 엔트로피
4. 쿨백-라이블러 발산(Kullback-Leibler divergence, KL divergence)
4.1 머신러닝의 목표
- 새로운 입력 데이터가 들어와도 예측이 잘되도록
- 모델의 확률 분포를 데이터의 실제 확률 분포에 가깝게 만드는 것
4.2 머신러닝 모델 종류
- 결정모델 (discriminative model):
- 데이터의 실제 분포를 모델링하지 X, 결정경계를 학습
- 결과값이<0 -> class1, 결과값이>0 -> class2
- 생성모델(generative model) :
- 데이터와 모델로부터 도출할 수 있는 여러 확률 분포와 베이즈 이론을 이용해서 데이터의 실제 분포를 간접적으로 모델링
- 생성모델을 학습할 때는 두 확률 분포의 차이를 나타내는 지표 필요 => 쿨백-라이블러 발산(Kullback-Leibler divergence)4.3 쿨백 라이블러 연산
- P(x) : 데이터가 따르는 실제 확률 분포
- Q(x) : 모델이 나타내는 확률 분포
- P(x)를 기준으로 계산된 Q(x)의 평균 정보량 - P(x)를 기준으로 계산된 평균 정보량
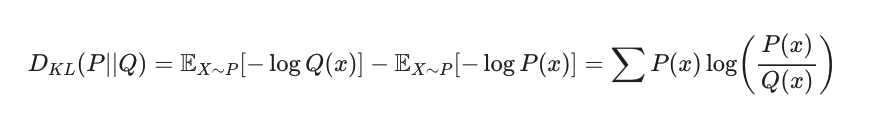
- 연속확률 변수의 경우
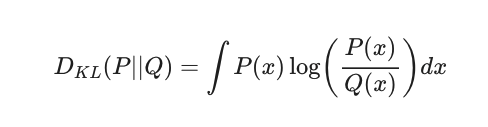
4.3 KL divergence의 특성

5. Cross Entorpy

- P(x)는 데이터의 실제 분포이므로, 우리가 바꿀 수 없는 고정된 값입니다.
- 따라서 바꿀 수 있는 부분은 Q(x)Q(x)에 관한 식이기 때문에 KL divergence를 최소화하는 문제는 빨간색 부분을 최소화하는 문제가 됩니다.
5.1 엔트로피와 교차 엔트로피, KL divergence 사이의 관계식

- 정답셋의 확률분포 P와 우리 모델의 추론 결과의 확률분포 Q 의 차이인 KL divergence를 최소화하는 것(우리 모델의 추론 결과가 정답셋과 최대한 유사하게 하는 것)은 교차 엔트로피(Cross Entropy)를 최소화하는 것이 수학적으로 같다.
5.2 Cross Entorpy Loss
- 손실함수 : 머신러닝에서 모델이 나타내는 확률 분포와 데이터가 따르는 실제 확률 분포 사이의 차이를 나타내는 함수
- 모델의 확률 분포는 파라미터에 따라 달라지기 때문에 손실 함수 역시 파라미터에 의해 결정
- 최소제곱법의 함수도 손실 함수
- 데이터가 이산적인 값을 가지는 분류(classification) 문제에서는 모델의 출력 결과가 로지스틱 함수(logistic function)
- 소프트맥스 함수(softmax function) : 분류 클래스가 2개인 로지스틱 함수를 클래스가 nn개일 때로 확장한 것
- cross entropy의 식

- 분류 문제에서 데이터의 라벨은 one-hot encoding을 통해 표현
- 클래스의 종류가 NN가지이고 특정 데이터가 nn번째 클래스에 속할 때, nn번째 원소만 1이고 나머지는 0으로 채운 NN차원 벡터
- 3개의 클래스 c_1,c_2,c_3c 가 존재하는 분류 문제에서 어떤 데이터의 출력값이 다음과 같다고 가정

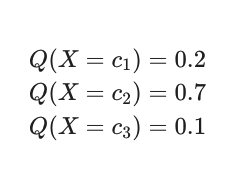
- 데이터가 실제로 2번 클래스에 속할 경우, 데이터의 실제 확률 분포는 one-hot encoding과 같은 [0,1,0][0,1,0]

- cross entropy를 사용하면 P(x)P(x)와 Q(x)Q(x)의 차이를 다음과 같이 계산 가능

- 분류 문제에서는 데이터의 확률 분포가 위와 같이 one-hot vector로 표현되기 때문에, P(x)P(x)와 Q(x)Q(x)의 차이를 cross entropy로 계산할 경우 계산이 간단해진다
6. Decision Tree와 Entropy
- 의사결정 트리는 가지고 있는 데이터에서 어떤 기준으로 전체 데이터를 나눴을 때 나누기 전보다 엔트로피가 감소하는지를 따져서,
- 엔트로피가 감소하면 그 만큼 정보 이득(Information Gain, IG)을 얻는다고 본다.